Statistics
Simple statistics can be good enough
Study of the mismatch between spatial environmental data and a commonly used statistical analysis suggests simpler statistics are sufficient in many cases.
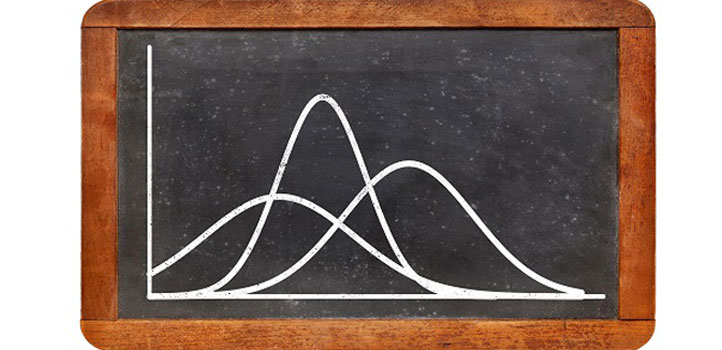
Gaussian distributions are simple and easy to understand, but for some data such as rainfall and wind speed, they can result in physically impossible tails to negative values.
© Marek Uliasz / Alamy Stock Photo
Environmental scientists and their statistician colleagues face a common dilemma: Do simpler statistical tests properly characterize a data set? And is it worth the effort to derive and apply statistical methods that are possibly better matched but more difficult to interpret? In most cases the path of least resistance wins, but the choice of a simple statistical basis can cast slight doubt on the validity of statistically derived study results.
KAUST researcher Marc Genton and his doctoral student Yuan Yan developed a framework to test exactly how inaccurate a mismatch between data and statistical analysis could be, and the results are surprising.
“Researchers tend to fit spatial data with a simple Gaussian model—the classic symmetric bell curve around the average value—even though data might have an asymmetric distribution with features that diverge from Gaussian,” says Yan. “We investigated the effect of the ‘non-Gaussianity’ of data on statistical estimation and prediction under the wrong Gaussian assumption.”
Gaussian distributions are generally intuitive, with an average value and standard deviations from the average that imply some narrow or broad distribution of data. They are widely applied and understood, both from a practitioner perspective and for nontechnical users. But, in many situations, particularly for environmental data, the distribution of data is skewed. Wind speed and rainfall, for example, cannot be less than zero, yet a Gaussian distribution with a small average value but extended distribution to higher values can have a tail at the lower end that extends to negative values—certainly wrong, but by how much?
One of the most important concepts in spatial statistical analyses is how strongly data influence each other when a certain distance apart, which is given by what is known as the covariance function. Genton and Yan set out to systematically study the effect of applying a Gaussian model to estimate the covariance function for non-Gaussian data.
“We developed a tailored simulation scheme to generate non-Gaussian spatial data with a given covariance structure,” says Genton. “We showed through our simulation study that when spatial data are non-Gaussian, the Gaussian likelihood estimator of covariance parameters still performs better than an alternative weighted least-squares estimator for data that are not heavily skewed.”
The finding suggests that the simple Gaussian model is in fact generally adequate for parameter estimation for spatial data in many cases, offering some comfort to spatial scientists about their choice of statistical approach.
References
- Yan, Y. & Genton, M.G. Gaussian likelihood inference on data from trans-Gaussian random fields with Matérn covariance function. Environmetrics 29, e2458 (2017).| article
You might also like

Statistics
Checking your assumptions
Statistics
Internet searches offer early warnings of disease outbreaks
Statistics
Joining the dots for better health surveillance

Statistics
Easing the generation and storage of climate data

Statistics
A high-resolution boost for global climate modeling

Applied Mathematics and Computational Sciences
Finer forecasting to improve public health planning

Bioengineering
Shuffling the deck for privacy
Bioengineering



