Applied Mathematics and Computational Sciences
Steep learning in mathematics of big waves
A better mathematical understanding of how big waves form could lead to better prediction of tsunami impacts.

Predicting the behavior of big waves, such as tsunamis, is exceptionally difficult, but a new mathematical approach could give a better picture of how they develop when they approach the shore.
“When a tsunami passes from deep water onto the continental shelf from ocean depths of thousands of meters to hundreds of meters or less, part of the wave energy is reflected backward and part is transmitted forward,” explains applied mathematician David Ketcheson. “The height of the wave is determined by the amount of transmission, but the actual height is always greater than that predicted by the transmission coefficient. One of the motivations for this work was to give a straightforward explanation of this discrepancy.”
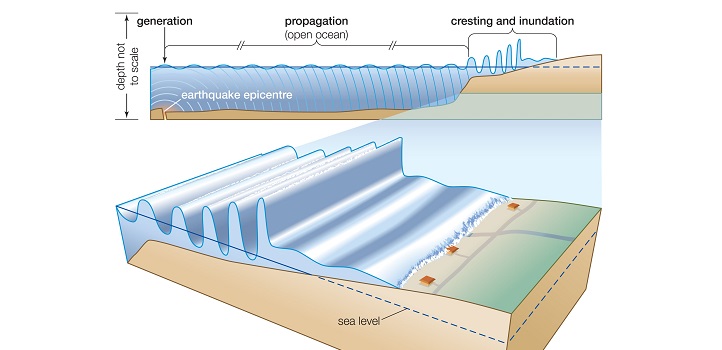
A tsunami passes from deep water onto the continental shelf, becoming higher as the shelf becomes shallower.
© Universal Images Group North America LLC / Alamy Stock Photo
The challenge arises because the edge of the continental shelf is not a sharp drop-off, but a steep slope that acts like a zone of gradual change. This is difficult to model because the reflection and transmission coefficients change incrementally as the wave moves across the upward slope. A mathematical principle called Green’s law can be used to capture the overall effect of this changing behavior when the continental slope is very gentle and the width of the slope region is large compared to the wave’s wavelength; but even this fails to accurately predict wave heights in complex real-world settings typified by neither gentle nor sharp slopes.
Ketcheson, working with Jithin George from Northwestern University and Randall LeVeque from the University of Washington, took another look at the shape of the edge of the continental shelf to explore whether a different mathematical approach could yield better results without resorting to a full numerical simulation based on detailed ocean floor bathymetry.
“In our analysis, we view this region as comprising infinitely many tiny interfaces, each of which leads to a tiny amount of reflection,” says Ketcheson. “Each reflection leads to additional reflections as it traverses backward, and each of those leads to further reflections, and so forth. To predict the shape and size of the developing waves, we need to keep track of the infinitely many paths that traverse the region over the continental slope.”
The researchers addressed this by considering first the wave path that involves no reflections, then paths with one reflection, then with two, and so on. A mathematical function called a path integral could then be used to evaluate the contribution from each set of paths. By computing all terms up to a specified number of reflections, the researchers showed that it is possible to obtain a good approximation of true wave development.
“Our work shows that as the continental slope gets steeper, the wave peak predicted by Green’s coefficient gets narrower, until in the limit of an infinitely steep slope, the peak vanishes,” says Ketcheson.
This understanding of tsunami propagation led to a new mathematical technique for solving the wave equation—one of the most fundamentally important mathematical models. As such, this approach could be used to increase understanding of many other kinds of waves, such as electromagnetic waves in the Earth’s atmosphere or sound waves in the ocean.
References
- George, J., Ketcheson, D. & LeVeque, R. Shoaling on steep continental slopes: relating transmission and reflection coefficients to Green’s law. Pure and Applied Geophysics, published 9 September (2019).| article
You might also like
Applied Mathematics and Computational Sciences
Bringing an old proof to modern problems

Applied Mathematics and Computational Sciences
Accounting for extreme weather to boost energy system reliability
Applied Mathematics and Computational Sciences
Past and future drought patterns across the Arabian Peninsula

Applied Mathematics and Computational Sciences
New pattern for underwater resonators

Applied Mathematics and Computational Sciences
Finer forecasting to improve public health planning

Applied Mathematics and Computational Sciences
Global look at sex differences in young people's mortality

Applied Mathematics and Computational Sciences
Going likelihood-free with neural networks
Applied Mathematics and Computational Sciences




